2021. 1. 25. 17:34ㆍ코딩 테스트/개념 학습 및 정리
1. 자료구조
1) 자료구조
자료를 저장하기 위한 구조이다. 목적에 맞는 구조를 디자인하는 것이 가장 중요하다.
- 변수도 자료구조이다.
- 배열은 특정 위치의 원소를 바로 알 수 있지만 원소의 추가 및 삭제가 불편하다는 점이 있다.
- Linked List는 원소의 삽입과 삭제가 빠르지만 특정 위치의 원소를 알기 쉽지 않다.
2) 캡슐화, 구조체
자료구조를 사용하는 사람은 자료구조가 어떻게 동작하는지 알 필요가 없고 알아서도 안된다. 즉, 내부가 감쳐져있다. 반면 구조체는 캡슐화를 구현하기 위한 문법으로 실체가 보이지 않는다. 하나의 값을 가지는 타입을 정의를 하며, Java에서는 클래스를 이용한다.
2. 기초 자료구조
1) 스택 (LIFO)
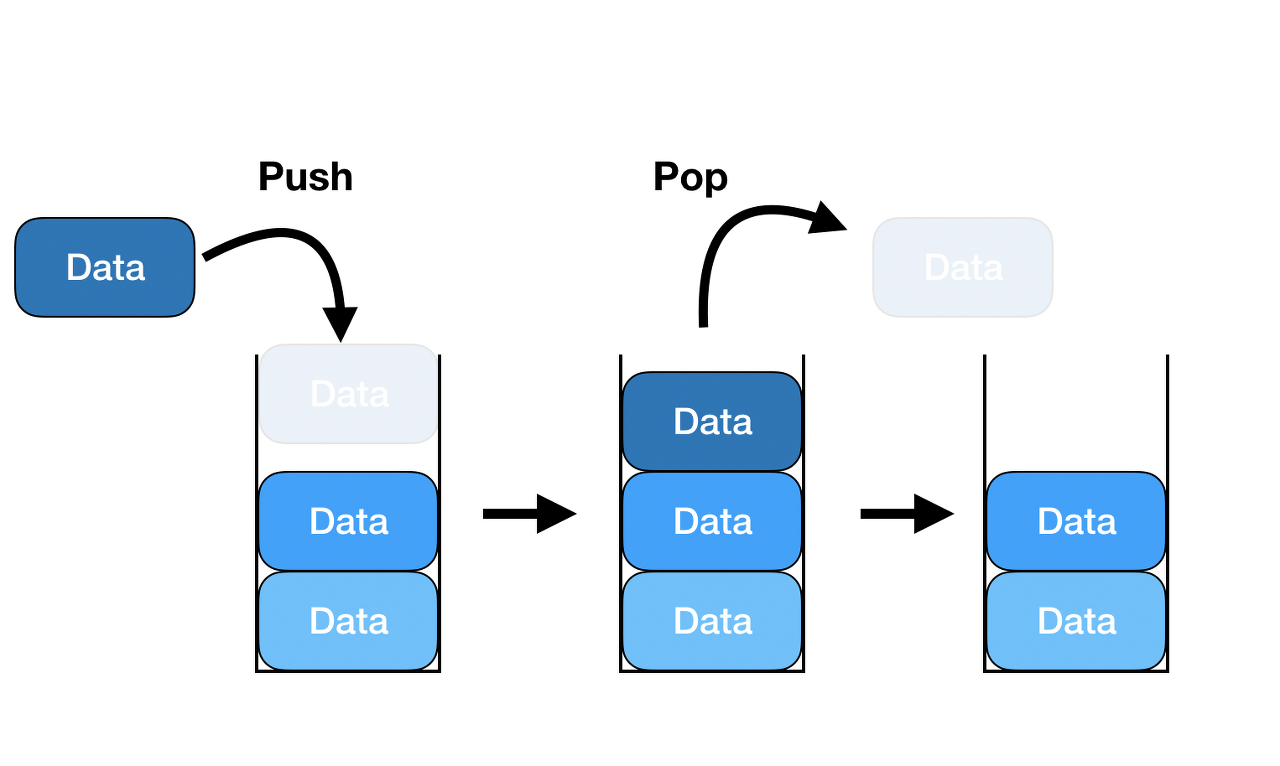
선형 자료로 Last In First Out, 가장 최근에 삽입한 원소가 먼저 나오는 구조이다. 스택의 활용은 다음과 같다
- 상태 저장 (미로 찾기)
- 콜 스택, 스케쥴링 (함수 호출을 추적, 재귀 함수)
interface Stack {
boolean isEmpty();
boolean isFull();
void push(char item);
char pop();
char peek();
void clear();
}
class ArrayStack implements Stack {
private int top;
private int stackSize;
private char[] stackArr;
public ArrayStack(int stackSize) {
this.top = -1;
this.stackSize = stackSize;
this.stackArr = new char[this.stackSize];
}
@Override
public boolean isEmpty() {
return top == -1;
}
@Override
public boolean isFull() {
return top == this.stackSize-1;
}
@Override
public void push(char item) {
if(isFull()) System.out.println("Stack is full");
else {
stackArr[++top] = item;
System.out.println("Inserted Item: " + item);
}
}
@Override
public char pop() {
if(isEmpty()) {
System.out.println("Stack is already empty");
return 0;
}
else {
System.out.println("Deleted item: " + stackArr[top]);
return stackArr[top--];
}
}
@Override
public char peek() {
if(isEmpty()) {
System.out.println("Stack is already empty");
return 0;
} else {
System.out.println("Peeked item: " + stackArr[top]);
return stackArr[top];
}
}
@Override
public void clear() {
if(isEmpty()) System.out.println("Stack is already empty");
else {
top = -1;
stackArr = new char[this.stackSize];
System.out.println("Stack is clear");
}
}
public void printStack() {
if(isEmpty()) System.out.println("Stack is already empty");
else {
System.out.println("Stack elements: ");
for(int i = 0; i <= top; i++) {
System.out.print(stackArr[i] + " ");
}
System.out.println();
}
}
}
public class Main {
public static void main(String[] args) {
int stackSize = 5;
ArrayStack arrStack = new ArrayStack(stackSize);
arrStack.push('A');
arrStack.push('B');
arrStack.push('C');
arrStack.printStack();
arrStack.pop();
arrStack.pop();
arrStack.printStack();
arrStack.pop();
arrStack.pop();
arrStack.push('D');
arrStack.push('E');
arrStack.clear();
arrStack.printStack();
}
}※ 스택 오버플로우는 더 이상 스택에 넣지(push) 못할 때 더 넣으려는 시도를 하는 경우 발생하는 에러이다. 반면 스택 언더플로우는 데이터가 없는데도 빼려고(pop) 할 때 생기는 문제이다.
2) 큐 (FIFO)
선형 자료로 First In First Out, 가장 처음에 삽입한 원소가 먼저 나오는 구조이다. 큐는 스택과 달리, 상태의 의존관계가 없을 때, 스케쥴링(병렬화)에 사용된다.


길이가 정해진 배열을 기반으로 큐를 구현할 경우에는 Rear 포인터를 더 오른쪽으로 옮길 수 없는 상황에서 문제가 발생한다. 즉, 먼저 들어온 데이터가 참조되어 빈 공간임에도 활용하지 못하는 상황이 발생한다. 따라서 원형 큐를 이용하여 이 문제를 해결한다.
interface Queue {
boolean isEmpty();
boolean isFull();
void enqueue(char item);
char dequeue();
char peek();
void clear();
}
class ArrayQueue implements Queue {
private int front;
private int rear;
private int queueSize;
private char[] queueArr;
public ArrayQueue(int queueSize) {
this.front = 0;
this.rear = 0;
this.queueSize = queueSize;
this.queueArr = new char[queueSize];
}
@Override
public boolean isEmpty() {
return this.rear == this.front;
}
@Override
public boolean isFull() {
return (this.rear + 1) % this.queueSize == front;
}
@Override
public void enqueue(char item) {
if(isFull()) System.out.println("Queue is full");
else {
this.rear = (++rear) % this.queueSize;
this.queueArr[this.rear] = item;
System.out.println("Inserted item: " + item);
}
}
@Override
public char dequeue() {
if(isEmpty()) {
System.out.println("Queue is already empty");
return 0;
} else {
this.front = (++this.front) % this.queueSize;
System.out.println("Deleted item: " + this.queueArr[this.front % this.queueSize]);
return this.queueArr[this.front];
}
}
@Override
public char peek() {
if(isEmpty()) {
System.out.println("Queue is already empty");
return 0;
} else {
System.out.println("Peeked item: " + this.queueArr[this.front+1]);
return this.queueArr[(this.front+1) % this.queueSize];
}
}
@Override
public void clear() {
if(isEmpty()) System.out.println("Queue is already empty");
else {
this.front = 0;
this.rear = 0;
this.queueArr = new char[this.queueSize];
}
}
public void printQueue() {
if(isEmpty()) System.out.println("Queue is already empty");
else {
for(int i = front+1; i <= rear; i++) {
System.out.print(queueArr[i] + " ");
}
System.out.println();
}
}
}
public class Main {
public static void main(String[] args) {
ArrayQueue arrQueue = new ArrayQueue(5);
arrQueue.enqueue('A');
arrQueue.enqueue('B');
arrQueue.enqueue('C');
arrQueue.printQueue();
arrQueue.dequeue();
arrQueue.dequeue();
arrQueue.printQueue();
arrQueue.enqueue('D');
arrQueue.peek();
arrQueue.dequeue();
arrQueue.dequeue();
arrQueue.dequeue();
}
}3) 트리
트리는 일반적으로 대상 정보의 각 항목들을 계층적으로 연관되도록 구조화시키고자 할 때 사용하는 비선형 자료구조이다. 데이터 요소들의 단순한 나열이 아닌 부모-자식 관계의 계층적 구조로 표현이 된다. 트리는 그래프의 한 종류이며 사이클이 없다.
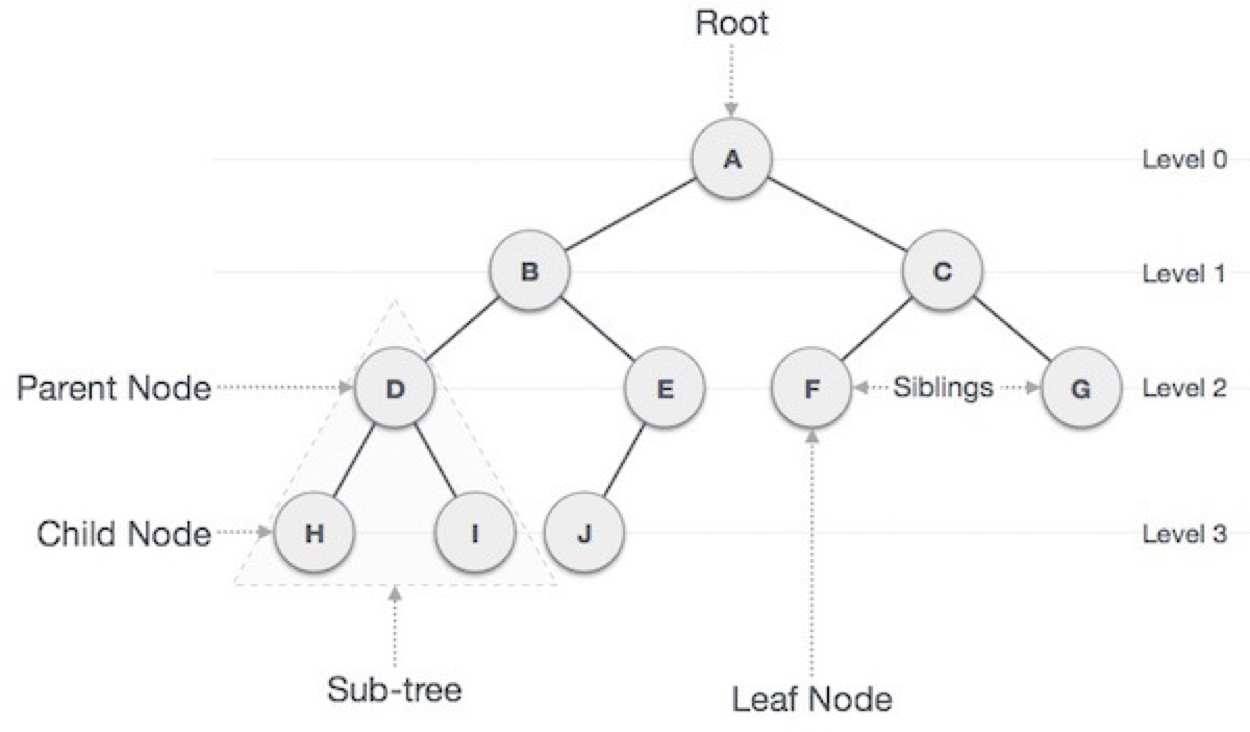
트리 순회에는 여러 방법이 있지만 보통 재귀적 성질을 이용하여 트리 내에의 자료를 확인을 한다. 이진 트리를 순회하는 방법은 다음과 같다.
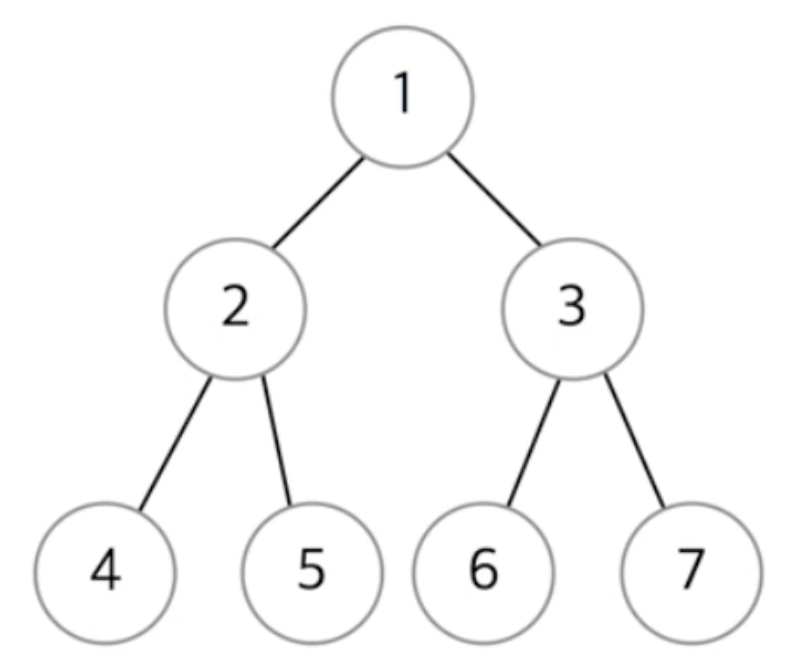
- 전위 순회 (Root - Left - Right) : 1 2 4 5 3 6 7
- 중위 순회 (Left - Root - Right) : 4 2 5 1 6 3 7
- 후의 순회 (Left - Right - Root) : 4 5 2 6 7 3 1
단순 배열을 이용하여 3개의 순회를 한다면 다음과 같다.
import java.io.*;
import java.util.StringTokenizer;
public class Main {
private static int[][] tree;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
tree = new int[n][2];
for(int i = 0; i < n; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
// 노드 a의 왼쪽 자식노드가 b, 오른쪽 자식노드가 c라는 뜻
// 자식노드가 존재하지 않을 경우에는 -1
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
tree[a][0] = b; // left
tree[a][1] = c; // right
}
preOrder(0);
System.out.println();
inOrder(0);
System.out.println();
postOrder(0);
br.close();
}
public static void preOrder(int x) { // 전위
if(tree[x][0] == -1 && tree[x][1] == -1) System.out.print(x + " ");
else {
System.out.print(x + " ");
if(tree[x][0] != -1) {
preOrder(tree[x][0]);
}
if(tree[x][1] != -1) {
preOrder(tree[x][1]);
}
}
}
public static void inOrder(int x) { // 중위
if(tree[x][0] == -1 && tree[x][1] == -1) System.out.print(x + " ");
else {
if(tree[x][0] != -1) {
inOrder(tree[x][0]);
}
System.out.print(x + " ");
if(tree[x][1] != -1) {
inOrder(tree[x][1]);
}
}
}
public static void postOrder(int x) { // 후위
if(tree[x][0] == -1 && tree[x][1] == -1) System.out.print(x + " ");
else {
if(tree[x][0] != -1) {
postOrder(tree[x][0]);
}
if(tree[x][1] != -1) {
postOrder(tree[x][1]);
}
System.out.print(x + " ");
}
}
}
/*
6
0 1 2
1 3 4
2 -1 5
3 -1 -1
4 -1 -1
5 -1 -1
*/조금 더 응용한다면 다음과 같이 설계할 수 있다.
class Node {
int data;
Node left;
Node right;
}
class Tree {
public Node root;
public void setRoot(Node node) {
this.root = node;
}
public Node getRoot() {
return root;
}
public Node createNode(Node left, int data, Node right) {
Node node = new Node();
node.data = data;
node.left = left;
node.right = right;
return node;
}
public void preOrder(Node node) { // 전위 순회 (Root - Left - Right)
if(node != null) {
System.out.println(node.data);
preOrder(node.left);
preOrder(node.right);
}
}
public void inOrder(Node node) { // 중위 순회 (Left - Root - Right)
if(node != null) {
inOrder(node.left);
System.out.println(node.data);
inOrder(node.right);
}
}
public void postOrder(Node node) { // 후위 순회 (Left - Right - Root)
if(node != null) {
postOrder(node.left);
postOrder(node.right);
System.out.println(node.data);
}
}
}
public class Main {
public static void main(String[] args) {
/*
이진 트리 형태
1
/ \
2 3
/ \
4 5
*/
Tree t = new Tree();
Node n4 = t.createNode(null, 4, null);
Node n5 = t.createNode(null, 5, null);
Node n2 = t.createNode(n4, 2, n5);
Node n3 = t.createNode(null, 3, null);
Node n1 = t.createNode(n2, 1, n3);
t.setRoot(n1);
t.inOrder(t.getRoot());
}
}
4) 우선순위 큐, 힙
우선순위 큐는 원소를 제거할 시, 가장 우선순위가 높은 원소를 제거하는 구조이다. 우선 순위가 가장 큰 것을 빠르게 찾기 위한 목적을 지니고 있다.
우선순위 큐는 제일 단순하게 배열로 구현이 가능하다.
interface Queue {
void enqueue(int item);
void dequeue();
int peek();
}
class PriorityQueue implements Queue {
private int queueIdx;
private int queueSize;
private int[] queueArr;
public PriorityQueue(int queueSize) {
this.queueIdx = 0;
this.queueSize = queueSize;
this.queueArr = new int[queueSize];
}
@Override
public void enqueue(int item) {
queueArr[queueIdx++] = item;
}
@Override
public void dequeue() {
int max = 0;
int maxIdx = 0;
for(int i = 0; i < queueIdx; i++) {
if(queueArr[i] > max) {
max = queueArr[i];
maxIdx = i;
}
}
for(int i = maxIdx; i < queueIdx; i++) {
queueArr[i] = queueArr[i+1];
}
queueIdx--;
}
@Override
public int peek() {
int max = 0;
for(int i = 0; i < queueIdx; i++) {
if(queueArr[i] > max) {
max = queueArr[i];
}
}
return max;
}
}
public class Main {
public static void main(String[] args) throws IOException {
PriorityQueue pQueue = new PriorityQueue(5);
pQueue.enqueue(1);
pQueue.enqueue(8);
pQueue.enqueue(7);
pQueue.enqueue(5);
System.out.println(pQueue.peek());
pQueue.dequeue();
System.out.println(pQueue.peek());
pQueue.dequeue();
System.out.println(pQueue.peek());
pQueue.dequeue();
System.out.println(pQueue.peek());
}
}배열로 구현을 한다면 대부분 삽입할 때 O(1), 삭제 시 O(n)의 시간복잡도를 가지게 된다. 하지만 만약 100000개를 모두 넣고 빼는 경우에는 삽입 시 O(1)이 걸리지만, 삭제 시 O(n^2) 크기의 어마어마한 시간 복잡도를 가지게 된다. 즉, 배열을 이용하여 우선순위 큐를 구현하는 방법은 비효율적일 수 있다.
이러한 배열의 비효율성은 트리(힙)를 이용하여 효율적으로 구현할 수 있다. 최소힙은 부모의 값이 항상 자식보다 작으며 최대힙은 부모의 값이 항상 자식보다 큰 완전 이진 트리 자료구조이다. 즉, 우선순위가 가장 작은 값이라고 한다면, 부모일 수록 우선순위가 높다.
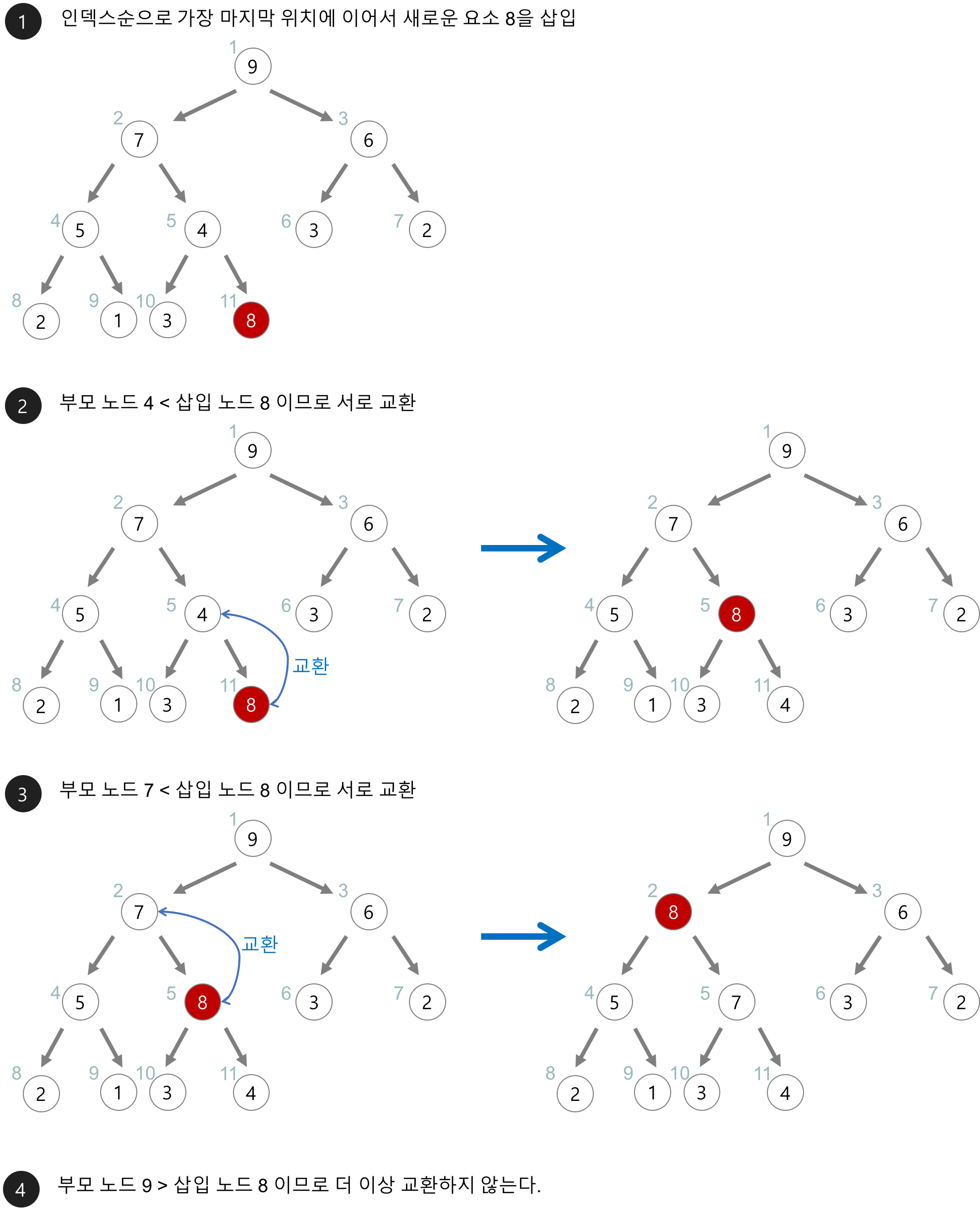
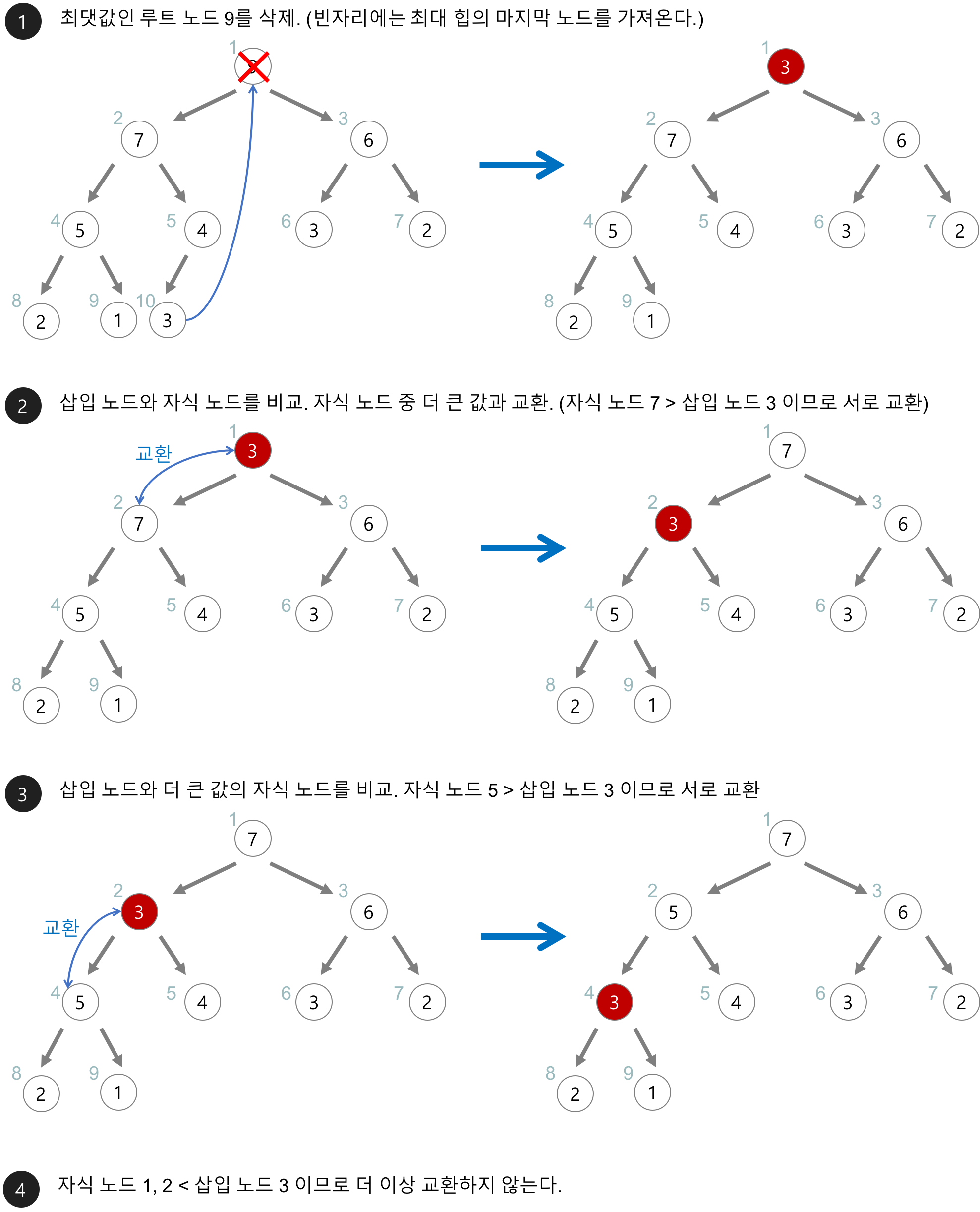
힙의 삽입 연산의 시간복잡도는 이진 트리의 높이와 관련이 있다.
- 노드의 개수가 1일 때 높이는 1
- 노드의 개수가 2일 때 높이는 2
- 노드의 개수가 3일 때 높이는 2
- 노드의 개수가 4일 때 높이는 3
- 과정 반복
- 높이가 1씩 커질 수록 노드의 개수는 2배
즉, 노드의 개수가 n개 일 때, 완전 이진 트리의 높이는 log n이 된다. 여기서 데이터를 삽입한다고 가정했을 때, 삽입된 위치에서부터 위로 비교하면서 올라가는데 걸리는 시간은 아무리 비교를 하면서 위로 올라가도 트리의 높이, O(log n)만큼 걸린다. 삭제를 하는 경우도 동일하다. 마지막 요소를 Root로 올린 뒤 아래로 내려가면서 비교를 하기 때문에 트리의 높이만큼의 시간복잡도가 걸린다.
배열로 우선 순위 큐를 구현하는 것보다 까다로운 점이 있지만, 효율과 성능 차원에서 본다면 힙이 뛰어나다는 것을 확인할 수 있다.
interface Queue {
void enqueue(int item);
void dequeue();
int peek();
}
class PriorityQueue implements Queue {
private int queueIdx;
private int queueSize;
private int[] queueArr;
public PriorityQueue(int queueSize) {
this.queueIdx = 1;
this.queueSize = queueSize;
this.queueArr = new int[queueSize];
}
@Override
public void enqueue(int item) {
queueArr[queueIdx++] = item;
int idx = queueIdx-1;
while(idx > 0) {
if (queueArr[idx] < queueArr[idx / 2]) {
int temp = queueArr[idx];
queueArr[idx] = queueArr[idx / 2];
queueArr[idx / 2] = temp;
} else break;
idx /= 2;
}
}
@Override
public void dequeue() {
// 마지막 요소를 Root로 이동
queueArr[1] = queueArr[queueIdx-1];
queueArr[queueIdx-1] = 0;
queueIdx--;
int idx = 1;
while(true) {
/*
자식 노드가 모두 없을 경우
- 왼쪽 노드의 번호가 전체 노드의 수보다 작을 경우
자식 노드가 왼쪽만 있을 경우
- 완전 이진 트리에서 오른쪽만 있는 경우는 성립하지 않음
- 왼쪽 노드의 번호가 1 이상, 전체 노드의 수보다 작은 경우
- 오른쪽 노드의 번호가 전체 노드의 갯수보다 크거나 같을 경우
자식 노드가 모두 있을 경우
- 왼쪽 노드와 오른쪽 노드 중 우선 순위가 높은 노드 비교
*/
int pIdx = -1; // 우선 순위가 높은 노드 번호
if(queueIdx <= idx*2) break; // 자식 노드가 모두 없을 경우
if(idx*2 >= 1 && idx*2 < queueIdx && idx*2+1 >= queueIdx) { // 자식 노드가 왼쪽만 있을 경우
pIdx = idx * 2;
} else { // 자식 노드가 모두 있을 경우
if (queueArr[idx * 2] < queueArr[idx * 2 + 1]) {
pIdx = idx * 2;
} else {
pIdx = idx * 2 + 1;
}
}
if(queueArr[idx] > queueArr[pIdx]) { // 부모가 자식보다 클 경우
int temp = queueArr[idx];
queueArr[idx] = queueArr[pIdx];
queueArr[pIdx] = temp;
idx = pIdx;
} else break;
}
}
@Override
public int peek() {
return queueArr[1];
}
}
public class Main {
public static void main(String[] args) {
PriorityQueue pQueue = new PriorityQueue(100);
pQueue.enqueue(3);
pQueue.enqueue(1);
pQueue.enqueue(2);
System.out.println(pQueue.peek());
pQueue.dequeue();
System.out.println(pQueue.peek());
pQueue.dequeue();
System.out.println(pQueue.peek());
pQueue.dequeue();
}
}
Java에서는 우선순위 큐에 대한 지원을 한다. 단, 제네릭 타입이 사용자가 정의한 객체일 경우 Comparable의 compareTo를 구현을 통해 우선순위를 정해주어야 올바르게 실행할 수 있다. 우선순위 큐의 Offer는 큐 한쪽 끝에 차곡차곡 쌓는데, 이때 추가되는 객체를 Comparable 인터페이스로 업캐스팅을 진행하여 우선순위를 정한다. 따라서 Comparable을 implement하지 않아 구현되어 있지 않다면 ClassCastException이 발생한다.
public class Student implements Comparable<Student>{
private String name;
private int age;
public Student(String name, int age) {
this.name = name;
this.age = age;
}
@Override
public int compareTo(Student target) {
return this.age <= target.age ? 1 : -1; //내림차순
}
public String toString() {
return "이름 : " + name + ", 나이 :" + age;
}
}
public class Main {
public static PriorityQueue<Student> getPriorityQueueOfStudents() {
PriorityQueue<Student> priorityQueue = new PriorityQueue<>();
priorityQueue.offer(new Student("A", 30));
priorityQueue.offer(new Student("B", 30));
priorityQueue.offer(new Student("C", 29));
priorityQueue.offer(new Student("D", 31));
priorityQueue.offer(new Student("E", 27));
return priorityQueue;
}
public static void main(String [] args) {
PriorityQueue<Student> priorityQueue = getPriorityQueueOfStudents();
while(!priorityQueue.isEmpty()) {
System.out.println(priorityQueue.poll());
}
}
}
/*
이름 : D, 나이 :31
이름 : A, 나이 :30
이름 : B, 나이 :30
이름 : C, 나이 :29
이름 : D, 나이 :27
*/
'코딩 테스트 > 개념 학습 및 정리' 카테고리의 다른 글
| [개념 학습 및 정리] 분할 정복법 (0) | 2021.01.28 |
|---|---|
| [개념 학습 및 정리] 문제 해결 (0) | 2021.01.28 |
| [개념 학습 및 정리] 이진 탐색, Parametric Search (0) | 2021.01.20 |
| [개념 학습 및 정리] 고급 정렬 (0) | 2021.01.18 |