[필수 문제] SCC
2021. 2. 15. 14:15ㆍ코딩 테스트/필수 문제
1. 문제
SCC (Strongly Connected Component)란, 방향성 그래프가 주어질 때 정점을 여러 집합으로 나누는 기법으로써, 같은 집합에 속해있는 정점끼리는 서로 왔다갔다 할 수 있어야 한다. 아래 그림은 그래프의 예제와, 이 그래프에서 SCC를 구한 예제이다.
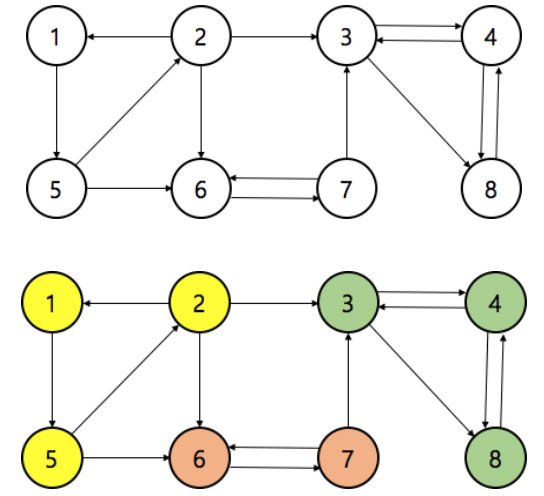
아래 그림처럼, 정점을 {1, 2, 5}, {6, 7}, {3, 4, 8} 의 3개의 집합으로 나누게 되면, 같은 집합에 속한 정점들끼리는 모두 왔다갔다 할 수 있다. 그래프가 주어질 때, SCC를 구하였을 때 얻을 수 있는 정점의 집합의 개수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 정점의 개수 N과 간선의 개수 M이 주어진다. ( 1 ≤ N ≤ 1,000, 1 ≤ M ≤ 100,000 ) 둘째 줄부터 간선의 정보가 주어진다. 각 줄은 두 개의 숫자 a, b로 이루어져 있으며, 이는 정점 a에서 정점 b로 향하는 간선이 존재한다는 의미이다. 각 정점의 번호는 1번부터 N번까지이다.
출력
주어진 그래프에서 SCC를 구하였을 때, 얻을 수 있는 정점의 집합의 개수를 출력한다.
예제 입력
8 14
1 5
2 1
2 3
2 6
3 4
3 8
4 3
4 8
5 2
5 6
6 7
7 3
7 6
8 4
예제 출력
3
2. 풀이
import java.io.*;
import java.util.*;
class Graph {
private ArrayList<ArrayList<Integer>> graph;
public Graph(int nodeSize) {
graph = new ArrayList<>();
for(int i = 0; i < nodeSize + 1; i++) {
graph.add(new ArrayList<>());
}
}
public ArrayList<Integer> getNode(int n) {
return graph.get(n);
}
public void put(int n, int m) {
graph.get(n).add(m);
// graph.get(m).add(n); // 방향 그래프이기 때문에 생략
}
}
public class Main {
private static final BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
private static final BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
private static int n;
private static int m;
private static Graph digraph; // 방향 그래프
private static Graph rdigraph; // 역방향 그래프
private static Graph result; // 각 그룹별 그래프 저장
private static boolean[] isVisited;
private static Stack<Integer> stack; // 역방향 그래프에 사용하기 위한 자료
public static void main(String[] args) throws IOException {
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
m = Integer.parseInt(st.nextToken());
digraph = new Graph(n);
rdigraph = new Graph(n);
result = new Graph(n);
isVisited= new boolean[n + 1];
stack = new Stack<>();
for(int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
digraph.put(a, b);
rdigraph.put(b, a);
}
for(int i = 1; i <= n; i++) { // 모든 정점에 대해서 탐색될 수 있도록 반복 (노드의 시작은 1이기에 1부터 시작)
if(!isVisited[i]) dfs(i); // 방향 그래프에 대해 dfs를 수행하고 탐색이 종료되는 점부터 스택에 push
}
Arrays.fill(isVisited, false); // 역방향 그래프에서도 사용하기 위해 초기화
int groupNum = 0;
while(!stack.isEmpty()) { // 역방향 그래프에 대해 dfs 수행
int v = stack.pop();
if(!isVisited[v]) {
rdfs(v, groupNum);
groupNum++;
}
}
bw.write(groupNum + "");
br.close();
bw.flush();
bw.close();
}
private static void dfs(int v) {
isVisited[v] = true;
for(int i = 0; i < digraph.getNode(v).size(); i++) {
int w = digraph.getNode(v).get(i);
if(!isVisited[w]) dfs(w);
}
stack.push(v);
}
private static void rdfs(int v, int groupNum) {
isVisited[v] = true;
result.getNode(groupNum).add(v);
for(int i = 0; i < rdigraph.getNode(v).size(); i++) {
int w = rdigraph.getNode(v).get(i);
if(!isVisited[w]) rdfs(w, groupNum);
}
}
}728x90
'코딩 테스트 > 필수 문제' 카테고리의 다른 글
| [필수 문제] 특정 최단거리 (0) | 2021.02.15 |
|---|---|
| [필수 문제] 최단거리 (0) | 2021.02.15 |
| [필수 문제] 목수의 미로 탈출 (0) | 2021.02.15 |
| [필수 문제] 미로 찾기 (0) | 2021.02.15 |