2021. 2. 1. 18:40ㆍ코딩 테스트/개념 학습 및 정리
1. 깊이 우선 탐색 (DFS)
1) 깊이 우선 탐색
깊이 우선 탐색은 스택을 이용하여 그래프를 순회하는 방법이다. '나'를 먼저 방문하고 그 다음으로 인접한 노드를 차례로 방문하는 방법이다. (단, 방문했던 노드를 방문하지 않는다.)
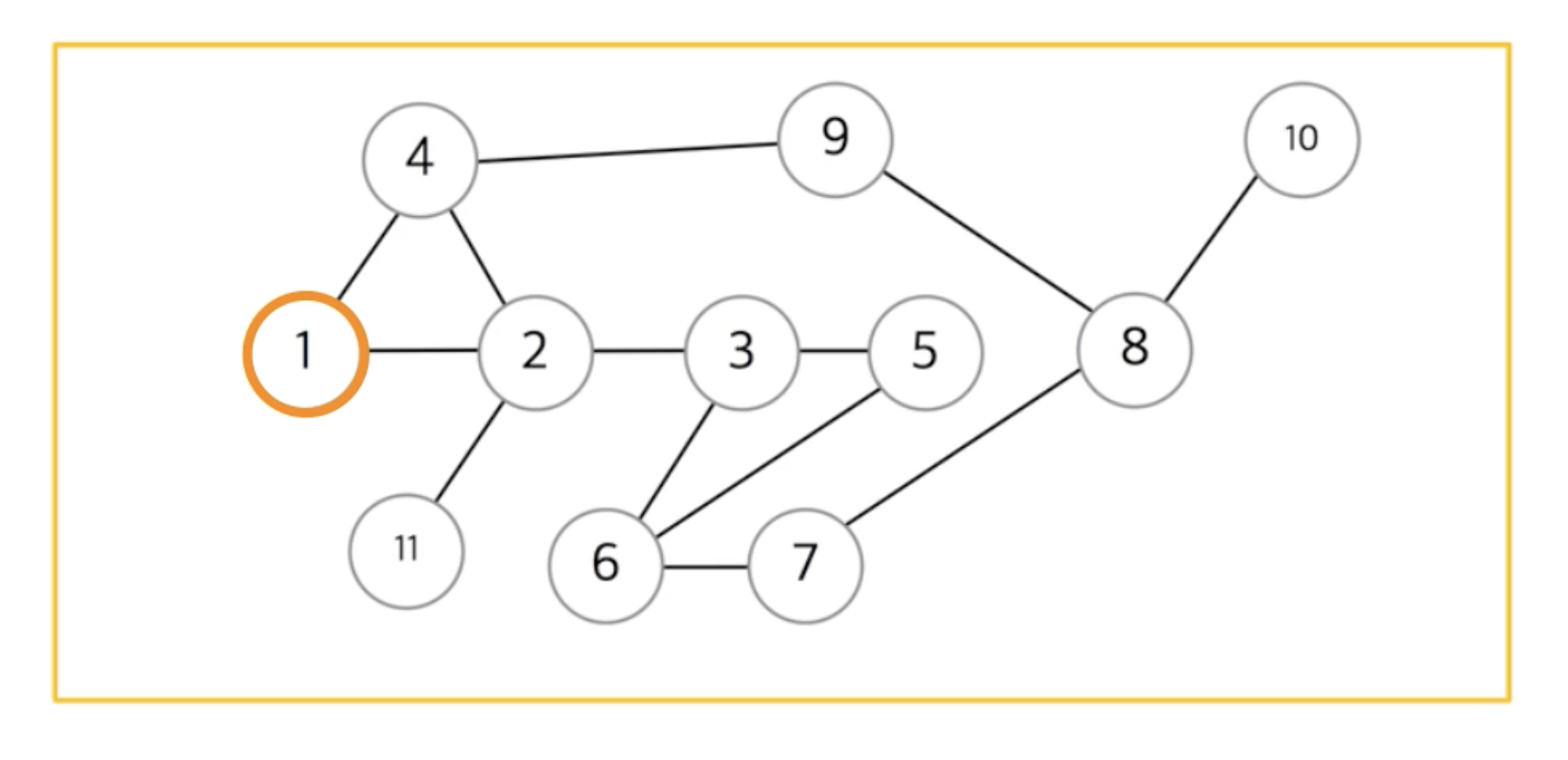
예를 들어, 다음과 같은 그림에서 인접한 노드가 여러개일 경우 노드 번호가 작은 노드부터 방문한다고 했을 때, 1을 시작으로 DFS한 결과는
'1 - 2 - 3 - 5 - 6 - 7 - 8 - 9 - 4 -10 - 11' 이 된다.
2) 구현
DFS(v, visited) - v는 시작점, visited는 방문한 노드 기록
- v를 방문했다고 처리
- v와 인접한 모든 w에 대해 다음을 반복
- 만약 w를 방문하지 않을 경우 DFS(w, visited)
- 방문 순서 반환
※ DFS는 재귀를 이용하며, 재귀는 스택 자료구조를 사용한다. 즉, DFS는 스택 자료구조를 이용한다.
import java.io.*;
import java.util.ArrayList;
import java.util.StringTokenizer;
class ListGraph {
private ArrayList<ArrayList<Integer>> listGraph;
public ListGraph(int listSize) {
this.listGraph = new ArrayList<ArrayList<Integer>>();
for(int i = 0; i < listSize + 1; i++) {
listGraph.add(new ArrayList<Integer>());
}
}
// 그래프 반환
public ArrayList<ArrayList<Integer>> getListGraph() {
return this.listGraph;
}
// 그래프의 특정 노드 반환
public ArrayList<Integer> getNode(int n) {
return this.listGraph.get(n);
}
// 그래프 추가 (양방향)
public void put(int n, int m) {
listGraph.get(n).add(m);
listGraph.get(m).add(n);
}
// 그래프 추가 (단방향)
public void putSingle(int n, int m) {
listGraph.get(n).add(m);
}
public void printListGraph() {
for(int i = 1; i < listGraph.size(); i++) {
System.out.print("정점 : " + i + "의 인접리스트");
for(int j = 0; j < listGraph.get(i).size(); j++) {
System.out.print("--> " + listGraph.get(i).get(j));
}
System.out.println();
}
}
}
public class Main {
private static int node;
private static int edge;
private static ListGraph listGraph;
private static boolean[] isVisited;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st_1 = new StringTokenizer(br.readLine());
node = Integer.parseInt(st_1.nextToken()); // 정점
int edge = Integer.parseInt(st_1.nextToken()); // 간선
isVisited = new boolean[edge];
listGraph = new ListGraph(edge);
for(int i = 0; i < edge; i++) {
StringTokenizer st_2 = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st_2.nextToken());
int b = Integer.parseInt(st_2.nextToken());
listGraph.put(a, b);
listGraph.put(b, a);
}
DFS(1);
bw.close();
br.close();
}
private static void DFS(int v) {
isVisited[v] = true;
System.out.print(v + " ");
for(int i = 0; i < listGraph.getNode(v).size(); i++) {
int w = listGraph.getNode(v).get(i);
if(!isVisited[w]) DFS(w);
}
}
}
/*
1 ----- 2 ------- 6
\ / \ /
\ / 4 --- 5
\ / / \
3 - 7 - 8 - 9
1 - 2 - 3 - 7 - 4 - 5 - 6 - 8 - 9
9 12
1 2
1 3
2 3
2 4
2 6
3 7
4 5
4 7
4 8
5 6
7 8
8 9
*/3) 시간 복잡도
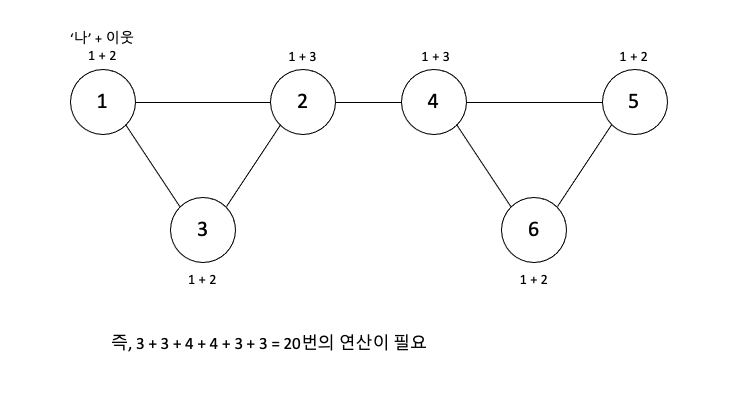
DFS의 시간 복잡도는 '나'를 방문하고, 인접한 모든 이웃에게 불어본다. 따라서 정점이 v개가 있을 때의 시간 복잡도는 다음과 같다.
- 노드 자신의 시간 복잡도 O(v)
- 이웃 노드의 시간 복잡도 O(deg(v)), 간선의 수 x 2
- 즉, O(v + deg(v))이며, 간선의 수는 상수이므로 O(v)
2. 너비 우선 탐색 (BFS)
1) 너비 우선 탐색
큐를 이용하여 그래프를 순회하는 방법이다. 인접한 노드들을 우선 모두 색칠해 두고 큐에 넣는 방식이다.
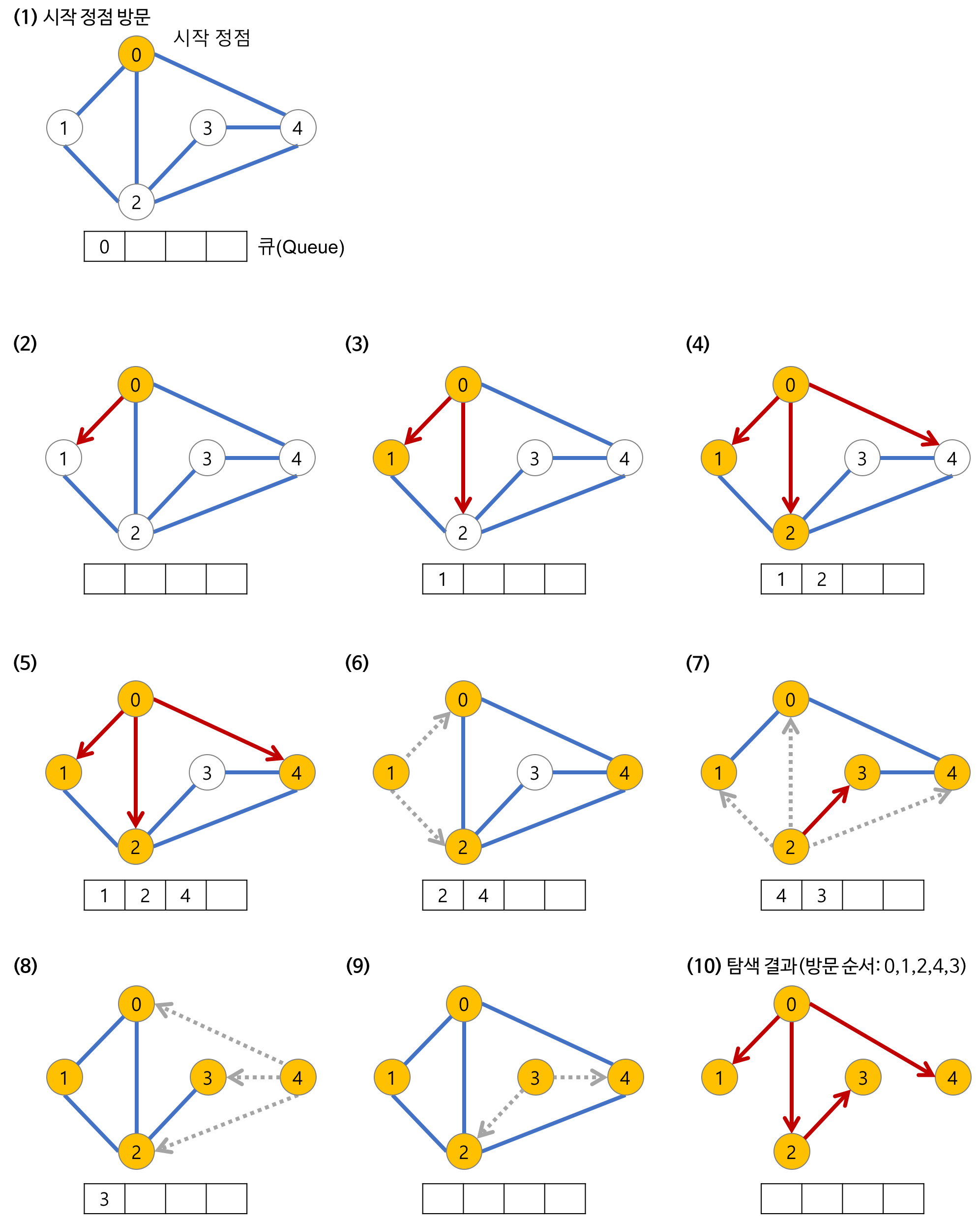
예를 들어, 다음과 같은 그림에서 인접한 노드가 여러개일 경우 노드 번호가 작은 노드부터 방문한다고 했을 때, 1을 시작으로 BFS한 결과는 다음과 같다.

- 시작 노드 삽입
| 1 |
- pop을 한 요소(1)를 기준으로 방문하지 않은 노드 삽입
| 2 | 4 |
- pop을 한 요소(2)를 기준으로 방문하지 않은 노드 삽입
| 4 | 3 | 11 |
- pop을 한 요소(4)를 기준으로 방문하지 않은 노드 삽입
| 3 | 11 | 9 |
- pop을 한 요소(3)를 기준으로 방문하지 않은 노드 삽입
| 11 | 9 | 5 | 6 |
- pop을 한 요소(11)를 기준으로 방문하지 않은 노드 삽입
| 9 | 5 | 6 |
- pop을 한 요소(9)를 기준으로 방문하지 않은 노드 삽입
| 5 | 6 | 8 |
- pop을 한 요소(5)를 기준으로 방문하지 않은 노드 삽입
| 6 | 8 |
- pop을 한 요소(6)를 기준으로 방문하지 않은 노드 삽입
| 8 | 7 |
- pop을 한 요소(8)를 기준으로 방문하지 않은 노드 삽입
| 7 | 10 |
- pop을 한 요소(7)를 기준으로 방문하지 않은 노드 삽입
- pop을 한 요소(10)를 기준으로 방문하지 않은 노드 삽입
따라서 순회 순서는 '1 - 2 - 4 - 3 - 11 - 9 - 5 - 6 - 8 - 7 - 10'이다.
2) 구현
BFS(v, visited) - v는 시작점, visited는 방문한 노드 기록
- v를 방문했다고 처리
- v와 인접한 모든 w에 대해 다음을 반복
- 만약 w를 방문하지 않을 경우 BFS(w, visited)
- 방문 순서 반환
import java.io.*;
import java.util.*;
class Graph {
private ArrayList<ArrayList<Integer>> graph;
public Graph(int nodeSize) {
this.graph = new ArrayList<>();
for(int i = 0; i < nodeSize+1; i++) {
this.graph.add(new ArrayList<Integer>());
}
}
public ArrayList<ArrayList<Integer>> getGraph() {
return this.graph;
}
public ArrayList<Integer> getNode(int n) {
return this.graph.get(n);
}
public void put(int n, int m) {
this.graph.get(n).add(m);
this.graph.get(m).add(n);
}
public boolean isAdjacent(int n, int m) {
for(int i = 0; i < graph.get(n).size(); i++) {
if(graph.get(n).get(i) == m) return true;
}
return false;
}
public void printGraph() {
for(int i = 1; i < graph.size(); i++) {
System.out.print("정점 " + i + "의 인접리스트");
for(int j = 0; j < graph.get(i).size(); j++) {
System.out.print("--> " + graph.get(i).get(j));
}
System.out.println();
}
}
}
public class Main {
private static int node;
private static int edge;
private static Graph graph;
private static boolean[] isVisited;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st_1 = new StringTokenizer(br.readLine());
node = Integer.parseInt(st_1.nextToken()); // 정점
edge = Integer.parseInt(st_1.nextToken()); // 간선
isVisited = new boolean[node+1];
graph = new Graph(node);
for(int i = 0; i < edge; i++) {
StringTokenizer st_2 = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st_2.nextToken());
int b = Integer.parseInt(st_2.nextToken());
graph.put(a, b);
}
bfs(1);
bw.close();
br.close();
}
public static void bfs(int start) {
Queue<Integer> queue = new LinkedList<>();
queue.offer(start);
isVisited[start] = true;
System.out.print(start + " ");
while(!queue.isEmpty()) {
int w = queue.poll();
for(int i = 1; i <= node; i++) {
if(graph.isAdjacent(i, w) && !isVisited[i]) {
queue.add(i);
isVisited[i] = true;
System.out.print(i + " ");
}
}
}
}
}
/*
1 ----- 2 ------- 6
\ / \ /
\ / 4 --- 5
\ / / \
3 - 7 - 8 - 9
1 - 2 - 3 - 4 - 6 - 7 - 5 - 8 - 9
9 12
1 2
1 3
2 3
2 4
2 6
3 7
4 5
4 7
4 8
5 6
7 8
8 9
*/
'코딩 테스트 > 개념 학습 및 정리' 카테고리의 다른 글
| [개념 학습 및 정리] 기초 그래프 알고리즘 (최소 신장 트리) (0) | 2021.02.10 |
|---|---|
| [개념 학습 및 정리] 기초 그래프 알고리즘 (다익스트라) (0) | 2021.02.06 |
| [개념 학습 및 정리] 그래프 (0) | 2021.02.01 |
| [개념 학습 및 정리] 동적 계획법 (0) | 2021.02.01 |