2021. 2. 6. 03:03ㆍ코딩 테스트/개념 학습 및 정리
1. 기초 그래프 알고리즘
- 최단경로 알고리즘
- Strongly Connected Component
- 최소 신장 트리
2. 최단경로
1) 최단경로
A에서 B까지 가는 최단경로를, 간선의 가중치(Weight)를 이용하여 구하는 알고리즘이다. 최단경로 알고리즘을 해결하는 대표적인 3가지 알고리즘은 다음과 같다.
- 다익스트라 알고리즘 : 하나의 정점에서 모든 정점까지의 최단거리를 구하는 알고리즘이다. 단, 간선의 가중치가 양수일 때만 사용한다.
- 플로이드 알고리즘 : 모든 정점에서 모든 정점까지의 최단거리를 구하는 알고리즘이다.
- 벨만포드 알고리즘 : 하나의 정점에서 모든 정점까지의 최단거리를 구하는 알고리즘이다. 단, 간선의 가중치가 양수, 음수 모두 가능하다.
※ 정점 x까지 최단거리로 가기 위해서는 그 직전까지의 최단거리로 가야한다는 점이 가장 중요하다.
2) 다익스트라 알고리즘
다익스트라 알고리즘은 최단 거리를 구할 때 이전까지 구했던 정보를 그대로 사용하는 알고리즘이다. 음의 간선은 존재하지 않으며 네비게이션, 지하철 노선 검색 등에 적합한 알고리즘이다.
구하는 방법은 다음과 같다.
- 출발 노드 설정 (시작점을 제외한 모든 정점 최단거리를 양의 무한대로 초기화, 시작점은 0)
- 출발 노드 기준으로 최소비용의 값을 저장
- 출발 노드를 제외한 나머지 노드 중 방문하지 않은 노드 중에서 가장 비용이 적은 노드 선택 (우선순위 큐)
- 해당 노드를 거쳐 특정한 노드로 가는 경우를 고려하여 최소 비용을 계속해서 갱신
1. 각 정점이 가지는 최단거리 값을 양의 무한대로 초기화한다. (시작점은 0)
2. 모든 정점을 큐에 삽입한다.

3. 최단거리 값이 가장 작은 정점 추출(우선순위 큐)을 한다. 가장 처음에는 시작점을 제외한 모든 정점들의 최단거리가 양의 무한대로 설정되어있기 때문에 당연히 시작점이 추출된다.
4. A가 나오기 때문에 A와 인접한 다른 모든 정점들을 방문하여 최단거리를 업데이트한다.
- B의 정점 : B에 있는 양의 무한대를 A에서 B로 가는 최단 경로이자 더 작은 값인 9로 업데이트
- D의 정점 : B와 동일하게 D의 최단거리인 14로 업데이트
- E의 정점 : B와 동일하게 E의 최단거리인 15로 업데이트
5. 최단거리 변경으로 인한 우선순위 큐의 루트 노드도 변경되었음을 인지한다.

6. A의 노드들에 대한 검사가 완료되었기에 다시 큐에서 최단거리가 가장 짧은 정점을 추출한다. (B의 최단거리가 가장 짧기에 B를 선택)
7. B와 연결된 정점들에 대한 최단거리 업데이트를 한다. C의 경우에는 '9 + 20 = 29'으로 업데이트된다.
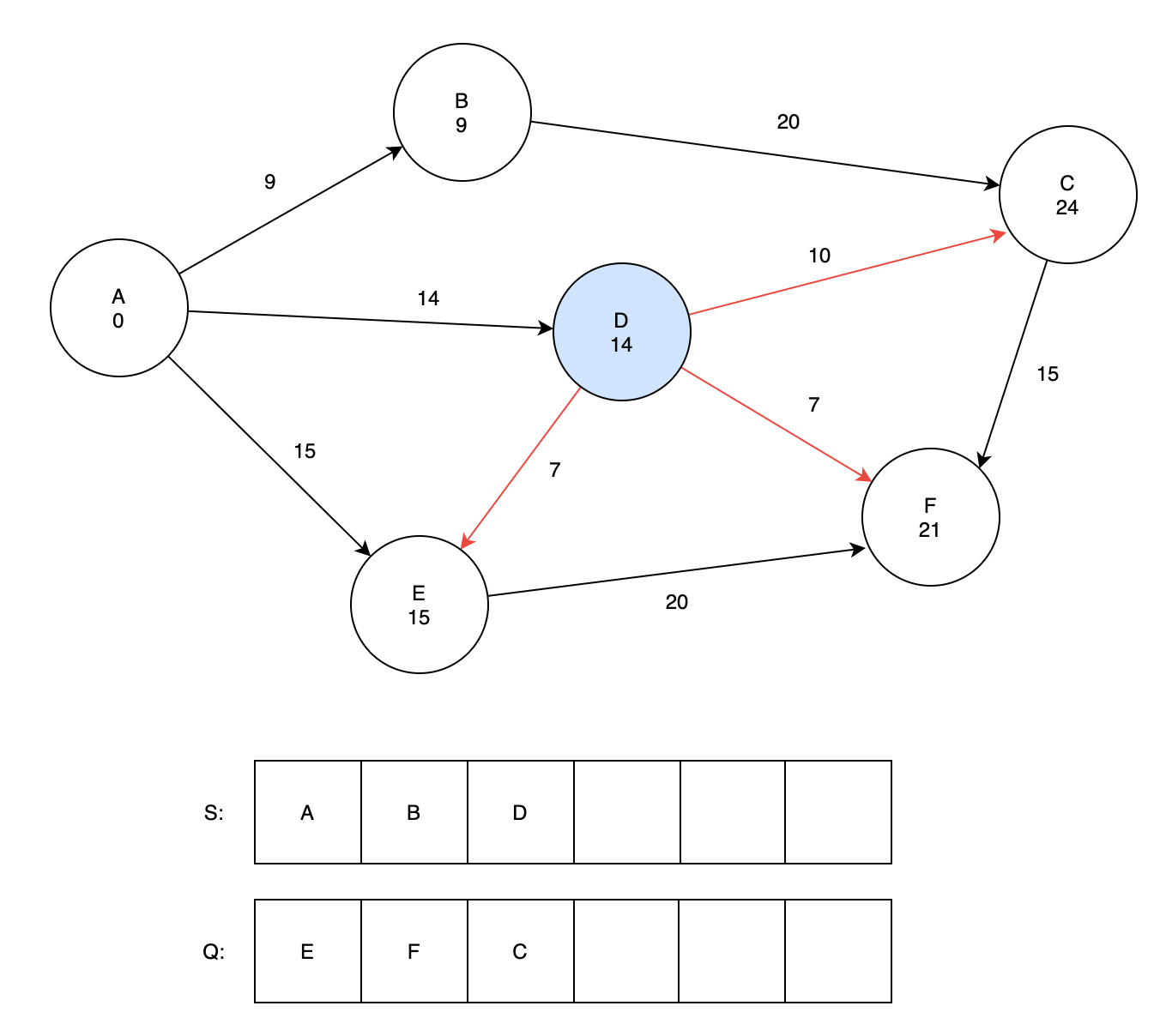
8. 큐에서 정점을 추출하게 되면 D가 추출이 되는데, 이도 동일하게 연결된 정점들을 업데이트해준다.
- E의 정점 : 정점 D를 거치는 최단경로는 '14 + 7 = 21'이지만, 이전에 저장된 최단 경로값이 계산된 값보다 작기에 유지
- F의 정점 : 정점 F에는 양의 무한대가 저장되어 있기에 '14 + 7 = 21'이 새로운 최단거리로 저장
- C의 정점 : 정점 C가 가지고 있는 최단거리가 29이지만 D를 거쳐 가는 경로가 '14 + 10 = 24'이기에 24로 업데이트

9. 다음으로 큐에서 추출된 정점 E와 연결된 정점은 F 하나이며, 저장되어있는 최단거리가 E를 통해 F로 가는 최단거리 '15 + 20 = 25'보다 작기 때문에 업데이트하지 않는다.

10. 다음으로 추출된 F는 연결된 정점이 없기에 바로 종료한다.

11. 다음으로 추출된 C의 경우 F와 연결되어 있으나, 기존에 저장된 최단 거리가 C를 거쳐 F로 가는 최단거리인 '24 + 15 = 39'보다 작기 때문에 업데이트를 하지 않는다.
3) 구현
구현시 주의해야할 점은, 다익스트라 알고리즘은 방향 그래프를 가정으로 둔다. 따라서 무방향 그래프가 주어진다면, 간선을 쪼개 방향 그래프로 변경해주어야한다. 또한 정점을 지날 수록 가중치가 증가한다는 사실을 전제로한 알고리즘으로, 전까지 계산한 최소가 최소라고 보장할 수 없기 때문에 가중치의 값이 음수여서는 안된다.
BFS를 기본으로 시작 정점에서 가까운 순서대로 방문을 한다. 매 순간 최선의 선택을 고르는 알고리즘으로는 탐욕 알고리즘을 사용한다. 우선순위 큐를 이용하여 매 순간 최단 거리 정점을 선택한다.
import java.io.*;
import java.util.*;
class Node implements Comparable<Node>{
private int node;
private int weight;
public Node(int node, int weight) {
this.node = node;
this.weight = weight;
}
@Override
public int compareTo(Node o) {
return weight - o.weight;
}
public int getNode() {
return this.node;
}
public int getWeight() {
return this.weight;
}
}
class Graph {
private ArrayList<ArrayList<Node>> graph;
public Graph(int nodeSize) {
graph = new ArrayList<>();
for(int i = 0; i < nodeSize + 1; i++) {
graph.add(new ArrayList<>());
}
}
public void put(int n, int m, int weight) {
graph.get(n).add(new Node(m, weight));
graph.get(m).add(new Node(n, weight));
}
public ArrayList<Node> getNode(int n) {
return graph.get(n);
}
}
public class Main {
private static int node;
private static int edge;
private static Graph graph;
private static boolean[] isVisited;
private static int[] dist;
private final static int INF = Integer.MAX_VALUE;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
node = Integer.parseInt(st.nextToken());
edge = Integer.parseInt(st.nextToken());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
graph = new Graph(node);
isVisited = new boolean[node + 1];
dist = new int[node + 1];
for(int i = 0; i < edge; i++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int w = Integer.parseInt(st.nextToken());
graph.put(a, b, w);
}
// 시작 노드에서 끝 노드까지의 최단 거리
dijkstra(start, end);
bw.write(dist[end] + "");
bw.flush();
bw.close();
br.close();
}
private static int dijkstra(int s, int e) {
Arrays.fill(dist, INF);
Arrays.fill(isVisited, false);
PriorityQueue<Node> pq = new PriorityQueue<>();
pq.add(new Node(s, 0)); // 시작 노드
dist[s] = 0;
while(!pq.isEmpty()) {
Node curPoint = pq.poll();
int curNode = curPoint.getNode();
int curWeight = curPoint.getWeight();
if(!isVisited[curNode]) {
isVisited[curNode] = true;
for(int i = 0; i < graph.getNode(curNode).size(); i++) {
int nextNode = graph.getNode(curNode).get(i).getNode();
int nextWeight = graph.getNode(curNode).get(i).getWeight();
if(!isVisited[nextNode] && dist[nextNode] > curWeight + nextWeight) {
dist[nextNode] = curWeight + nextWeight;
pq.add(new Node(nextNode, dist[nextNode]));
}
}
}
}
return dist[e];
}
}
/*
8개의 노드와 11개의 간선으로 이루어진 그래프
0번째 노드에서 시작하여 6번째 노드까지의 최단 거리
예제 입력
8 11 0 6
0 1 3
0 5 1
1 2 4
1 3 1
1 5 1
2 4 6
2 6 9
2 7 4
3 4 2
4 6 9
6 7 3
예제 출력
13
*/[참고] velog.io/@minhee/dijkstraalgorithm
'코딩 테스트 > 개념 학습 및 정리' 카테고리의 다른 글
| [개념 학습 및 정리] SCC (Strongly Connected Components) (0) | 2021.02.11 |
|---|---|
| [개념 학습 및 정리] 기초 그래프 알고리즘 (최소 신장 트리) (0) | 2021.02.10 |
| [개념 학습 및 정리] DFS, BFS (0) | 2021.02.01 |
| [개념 학습 및 정리] 그래프 (0) | 2021.02.01 |