2021. 2. 11. 01:49ㆍ코딩 테스트/개념 학습 및 정리
1. SCC (Stronlgy Connected Components)
1) SCC
SCC는 연결되어 있는 그래프들 끼리 나누는 알고리즘이다.
무방향 그래프로 표현한다면 다음과 같이 정의할 수 있다.

하지만 다음과 같은 방향성 그래프에서는 1에서 10으로 이동이 가능하나, 10에서 1로 갈 수 없기 때문에 무방향 그래프처럼 그룹을 나눌 수 없다.

따라서 방향성 그래프를 그룹별로 나누기 위해서는, 그룹 내의 노드가 서로 양방향으로 도달할 수 있는 길이 있어야 한다. 예를 들어 '1 - 2 - 3'에서 1과 2를 본다면, 1은 2로 이동이 가능하고, 2도 3을 거쳐 1로 이동이 가능한 구조여야 하나의 그룹으로 지정할 수 있다는 뜻이다. 즉, 하나의 그룹 내에 특정 두 개의 노드 x, y는 x에서 y로, y에서 x로 양방향 이동이 가능해야 묶을 수 있다는 뜻이다.

2) 코사라주 알고리즘
이렇듯, 서로 이동 가능한 그룹을 구하는 문제가 SCC이다. 그 중, SCC 문제를 풀 수 있는 대표적인 알고리즘으로는 코사라주 알고리즘이 있다. 코사라주 알고리즘의 큰 아이디어로는 메타 그래프를 만드는 것이다. 메타 그래프는 서로 이동 가능한 노드들로 묶어낸 그룹을 하나의 정점으로 생각하여 접근하는 방법이다.

3) 동작 예시
예를 들어, 어떠한 방법으로 메타 그래프의 마지막 그룹을 잡고, 그 그룹 내의 특정 노드 하나를 알려준다는 가정을 한다면 쉽게 이해할 수 있다.
1. 메타 그래프의 3번 그룹의 내부 노드 11을 알고 있다고 가정해본다.
- 11에서 시작하여 순회를 통해 12의 노드 확인 가능
- 확인된 그룹 삭제

2. 메타 그래프의 4번 그룹의 내부 노드 7을 알고 있다고 가정해본다.
- 7에서 시작하여 순회를 통해 8, 9, 10 노드 확인 가능
- 확인된 그룹 삭제

3. 이 과정을 반복하여 모든 그룹을 구할 수 있다.
문제는 어떠한 방법으로 메타 그래프의 마지막 그룹을 알아낼 것인지가 중요하다. 이 문제는 DFS를 통해 부모-자식 관계가 파악이 된다는 점을 이용하여 해결이 가능하다.
예를 들어, 2 그룹의 4 노드를 알고 있다고 가정한다면, DFS 순회 방법을 이용하여 5, 6, 11, 12 노드를 알 수 있다. 즉, 4에서 부터 순회를 시작하면 4에 속한 그룹 뿐만 아닌 그 그룹의 자식 그룹의 노드들도 모두 방문할 수 있다는 점이다. 다른 말로는, 4, 5, 6가 속한 그룹의 상위 그룹(메타 그래프 1과 4)에는 도달할 수 없다는 뜻이 된다.

이 때 그래프의 모든 간선의 방향을 모두 뒤집어, 메타 그래프의 방향을 변경해준다.

그렇게 되면 메타 그래프의 1과 4 그룹이 자식이 되면서 안보이게 된다. 따라서 2 그룹이 마지막 노드가 되는 모습을 확인할 수 있다.

요약하자면 다음과 같다.
- 그래프의 랜덤 노드를 선택 (위의 예시에서는 4 노드 사용)
- 선택된 노드에서 DFS 순회
- 선택된 노드의 그룹과 하위 그룹 정보를 획득
- 모든 간선의 방향을 반대로 뒤집어 메타 그래프 그룹간의 관계를 변경
- 변경된 관계를 확인했을 때, 선택된 노드의 그룹이 메타 그래프에서의 마지막 그룹이 됨을 확인
어떻게 그룹을 구하는지, 그룹을 구하는 과정에서 어떻게 메타 그래프의 마지막 그룹을 알아낼지에 대한 원리를 이해했다면, 이번에는 한번에 여러 그룹을 구하는 방법에 대해서 고민을 해보아야한다. 결론부터 말한다면, 한번에 여러 그룹을 구하는 방법은 빠져나오는 시간을 이용하면 해결이 가능하다.
다시 한번 위의 과정을 적용해 따라가 본다면 한번에 여러 그룹을 구하는 방법을 생각할 수 있다.
1. 랜덤으로 1 노드를 선택한다고 가정한다.

2. 1 노드에서 순회를 한다면 모든 노드를 알 수 있다.
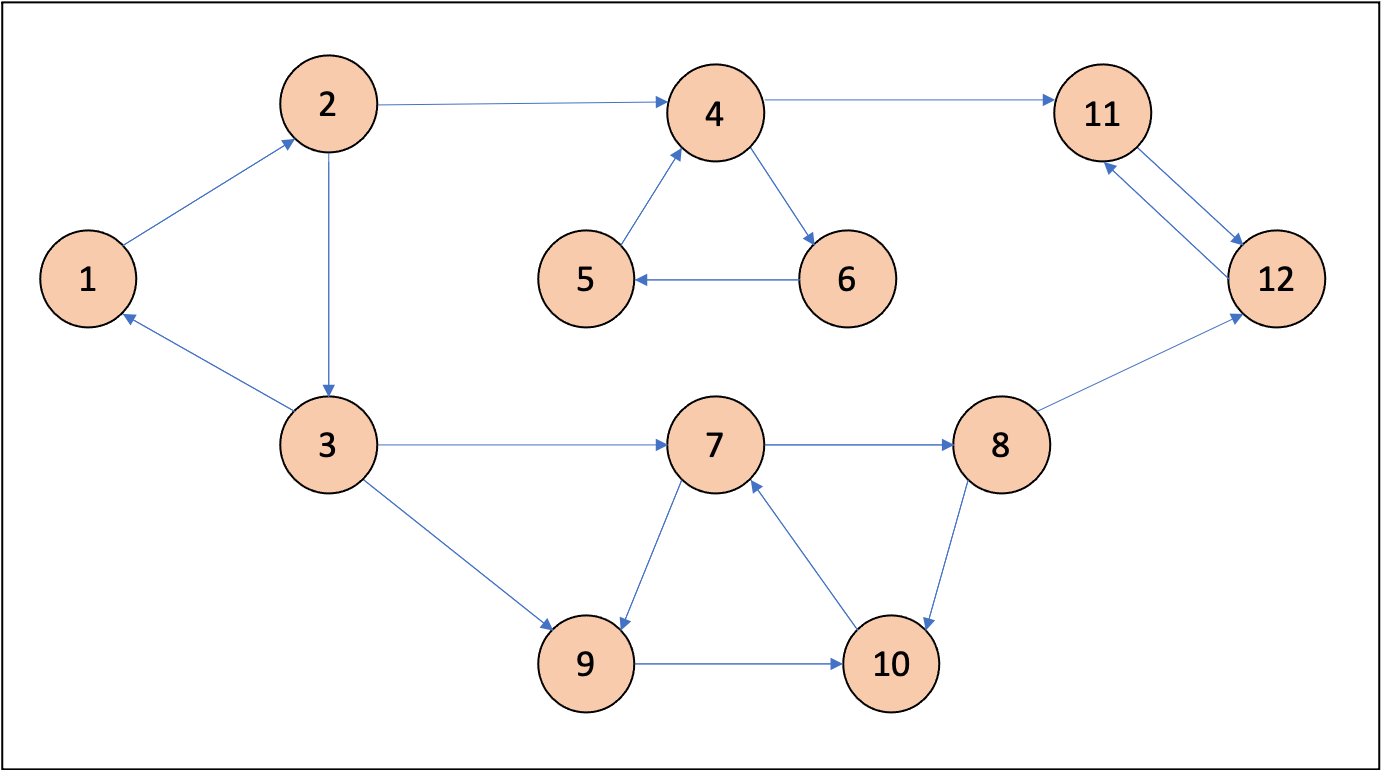

3. 모든 간선의 방향을 변경해준다.


4. '1 - 2 - 3' 그룹을 떼어낸다.
- '4 - 5 - 6'과 '7 - 8 - 9 - 10'이 메타 그래프의 말단 그룹이 된다.


결국, 마지막 '1 - 2 - 3' 노드를 떼어낸 후의 말단이 되는 그룹은 '4 - 5 - 6'과 '7 - 8 - 9 - 10'임을 알 수 있다. 그 다음에는 각각 말단이 되는 그룹의 내부 노드(4, 7 노드)를 통해 그룹을 나누면 된다. 이처럼 '1 - 2 - 3'을 떼어낸 이후에도 말단이 되는 그룹을 쉽게 찾을 수 있다는 점을 이용하여 한번에 여러 그룹을 구할 수 있다.
한번에 여러 그룹을 구하는 방법은 DFS를 이용하여 빠져나가는 시간을 활용하면 된다.
1. 1 노드에서 DFS를 적용하면 '1 - 2 - 3 - 7 - 8 - 12 - 11' 순으로 수행하게 된다.

2. 11 노드까지 도달하고 다시 돌아가면서 시간을 측정한다.

3. 메타 그래프 관점에서 본다면 각 그룹에서 걸리는 최대 시간을 비교한다면, 값이 작을 수록 말단에 있는 그룹임을 알 수 있다. 하지만 그래프 간선 방향을 바꾸는 동작을 수행하게 되면 값이 가장 큰 그룹이 가장 끝에 있는 그룹이 된다.

4) 동작 요약
- DFS를 통해 빠져나오는 시간을 기록
- 간선의 방향을 뒤집는다
- 기록한 시간이 큰 순서대로 순회하여 그룹을 분리
※ 시간 복잡도는 DFS 순회를 두번 수행하기에 O(V+E)만큼의 시간이 소요된다. 그만큼 굉장히 빠른 알고리즘이다.
5) 구현
import java.io.*;
import java.util.*;
class Graph {
private ArrayList<ArrayList<Integer>> graph;
public Graph(int nodeSize) {
graph = new ArrayList<>();
for(int i = 0; i < nodeSize + 1; i++) {
graph.add(new ArrayList<>());
}
}
public void put(int n, int m) {
graph.get(n).add(m);
// graph.get(m).add(n); // 방향 그래프이기에 생략
}
public ArrayList<Integer> getNode(int n) {
return graph.get(n);
}
}
public class Main {
private static int node;
private static int edge;
private static Graph digraph; // 방향 그래프
private static Graph rdigraph; // 역방향 그래프
private static Graph result;
private static boolean[] isVisited;
private static Stack<Integer> stack; // 역방향 그래프에 사용하기 위한 자료
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
node = Integer.parseInt(st.nextToken());
edge = Integer.parseInt(st.nextToken());
digraph = new Graph(node);
rdigraph = new Graph(node);
result = new Graph(node);
isVisited = new boolean[node + 1];
stack = new Stack<>();
for(int i = 0; i < edge; i++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
digraph.put(a, b);
rdigraph.put(b, a);
}
// 방향 그래프에 대해 dfs를 수행하고 탐색이 종료되는 점부터 스택에 push
dfs(1);
// 역방향 그래프에 사용하기 위해 초기화
Arrays.fill(isVisited, false);
// 역방향 그래프에 대해 dfs를 수행
int groupNum = 0;
while(!stack.isEmpty()) {
int v = stack.pop();
if(!isVisited[v]) {
rdfs(v, groupNum);
groupNum++;
}
}
bw.write("그룹의 개수: " + groupNum + "\n");
TreeMap<Integer, Integer> map = new TreeMap<>();
for(int i = 0; i < groupNum; i++) {
Collections.sort(result.getNode(i));
map.put(result.getNode(i).get(0), i); // 정렬된 그룹의 첫 번째 항(오름차순), 인덱스
}
StringBuilder sb = new StringBuilder();
sb.append("나뉜 그룹: \n");
map.keySet().forEach(key -> {
int value = map.get(key);
for(int i = 0; i < result.getNode(value).size(); i++) {
sb.append(result.getNode(value).get(i) + " ");
}
sb.append("\n");
});
bw.write(sb.toString());
bw.flush();
bw.close();
br.close();
}
private static void dfs(int v) {
isVisited[v] = true;
for(int i = 0; i < digraph.getNode(v).size(); i++) {
int w = digraph.getNode(v).get(i);
if(!isVisited[w]) dfs(w);
}
stack.push(v);
}
private static void rdfs(int v, int groupNum) {
isVisited[v] = true;
result.getNode(groupNum).add(v);
for(int i = 0; i < rdigraph.getNode(v).size(); i++) {
int w = rdigraph.getNode(v).get(i);
if(!isVisited[w]) rdfs(w, groupNum);
}
}
}
/*
예제 입력
12 18
1 2
2 3
2 4
3 1
3 7
3 9
4 6
4 11
5 4
6 5
7 8
7 9
8 10
8 12
9 10
10 7
11 12
12 11
예제 출력
그룹의 개수: 4
나뉜 그룹:
1 2 3
4 5 6
7 8 9 10
11 12
*/'코딩 테스트 > 개념 학습 및 정리' 카테고리의 다른 글
| [개념 학습 및 정리] 기초 그래프 알고리즘 (최소 신장 트리) (0) | 2021.02.10 |
|---|---|
| [개념 학습 및 정리] 기초 그래프 알고리즘 (다익스트라) (0) | 2021.02.06 |
| [개념 학습 및 정리] DFS, BFS (0) | 2021.02.01 |
| [개념 학습 및 정리] 그래프 (0) | 2021.02.01 |